 One of the most powerful and useful features of FC-i Counting Scale Series is ACAI, Automatic Counting Accuracy Improvement. It is not a new feature but a feature we had incorporated to the first generation of FC counting scales in order to maximize the accuracy of counting without sacrificing ease of use. However, to our bewilderment we are once in a while asked why it is there or even if it can be removed. The reason is simply that some operators do not understand how it works. Since the theory behind the ACAI involves some knowledge of statistical mathematics about errors, it sometimes discourages people to even try to understand what it is. I have always felt I wanted to come up with a simple explanation about it so that those who may not have taken advantage of it by regarding it a nuisance coined by some software wizard, can use it in a positive manner; though in actuality it is a result of the careful observation of how a counting scale is being used at workplaces.
One of the most powerful and useful features of FC-i Counting Scale Series is ACAI, Automatic Counting Accuracy Improvement. It is not a new feature but a feature we had incorporated to the first generation of FC counting scales in order to maximize the accuracy of counting without sacrificing ease of use. However, to our bewilderment we are once in a while asked why it is there or even if it can be removed. The reason is simply that some operators do not understand how it works. Since the theory behind the ACAI involves some knowledge of statistical mathematics about errors, it sometimes discourages people to even try to understand what it is. I have always felt I wanted to come up with a simple explanation about it so that those who may not have taken advantage of it by regarding it a nuisance coined by some software wizard, can use it in a positive manner; though in actuality it is a result of the careful observation of how a counting scale is being used at workplaces.
 While accurate and stable weighing or well-designed solid hardware is a must for a scale to do accurate counting, one basic norm for a counting scale is that the bigger internal resolution it has, the more accurate counting it gives. For instance, let’s take the example of a scale with internal resolution of one part by 3,000; in other words, a scale of 3kg capacity by 1 gram resolution. When one counts materials lighter than 1 gram per piece with this scale, for instance 0.1 gram apiece, it means 10 pieces make one gram. Thus when counting, the scale can detect a change in weight only when 5 or more pieces that are equal to the half of the scale’s increment are added. When you want to count up to 300 pieces, it can be 295 through 304 since the last digit stays zero because of the limitation of its internal resolution. The weighing result always has an error of +/- 5 pieces. Please refer to Counting Error and Count on Your Intelligence for a detailed explanation about this.
While accurate and stable weighing or well-designed solid hardware is a must for a scale to do accurate counting, one basic norm for a counting scale is that the bigger internal resolution it has, the more accurate counting it gives. For instance, let’s take the example of a scale with internal resolution of one part by 3,000; in other words, a scale of 3kg capacity by 1 gram resolution. When one counts materials lighter than 1 gram per piece with this scale, for instance 0.1 gram apiece, it means 10 pieces make one gram. Thus when counting, the scale can detect a change in weight only when 5 or more pieces that are equal to the half of the scale’s increment are added. When you want to count up to 300 pieces, it can be 295 through 304 since the last digit stays zero because of the limitation of its internal resolution. The weighing result always has an error of +/- 5 pieces. Please refer to Counting Error and Count on Your Intelligence for a detailed explanation about this.
 Infinite (internal) resolution is the solution to overcome the accuracy limitation mentioned above, however even that by itself is not sufficient. There is another error factor inherent in any counting situation. That is, the materials you want to count are not uniform in weight; some are lighter and others, heavier, or more specifically no materials weigh the same. In normal cases they follow what mathematicians define normal distribution, whose characteristics can be described by the average weight and standard deviation. In order to demonstrate this I weighed 100 A&D Clips, the results of which are shown in TABLE 1.
Infinite (internal) resolution is the solution to overcome the accuracy limitation mentioned above, however even that by itself is not sufficient. There is another error factor inherent in any counting situation. That is, the materials you want to count are not uniform in weight; some are lighter and others, heavier, or more specifically no materials weigh the same. In normal cases they follow what mathematicians define normal distribution, whose characteristics can be described by the average weight and standard deviation. In order to demonstrate this I weighed 100 A&D Clips, the results of which are shown in TABLE 1.
0.859 |
0.889 |
0.86 |
0.899 |
0.869 |
0.877 |
0.866 |
0.875 |
0.928 |
0.858 |
0.881 |
0.884 |
0.884 |
0.858 |
0.882 |
0.86 |
0.863 |
0.853 |
0.876 |
0.866 |
0.889 |
0.874 |
0.863 |
0.861 |
0.893 |
0.88 |
0.861 |
0.877 |
0.891 |
0.85 |
0.881 |
0.894 |
0.872 |
0.871 |
0.891 |
0.891 |
0.855 |
0.871 |
0.858 |
0.903 |
0.862 |
0.856 |
0.877 |
0.872 |
0.894 |
0.861 |
0.927 |
0.858 |
0.858 |
0.869 |
0.886 |
0.892 |
0.897 |
0.901 |
0.868 |
0.875 |
0.862 |
0.904 |
0.857 |
0.858 |
0.898 |
0.878 |
0.884 |
0.889 |
0.865 |
0.853 |
0.879 |
0.894 |
0.864 |
0.895 |
0.873 |
0.903 |
0.874 |
0.861 |
0.902 |
0.868 |
0.859 |
0.887 |
0.859 |
0.884 |
0.876 |
0.879 |
0.86 |
0.889 |
0.859 |
0.896 |
0.862 |
0.896 |
0.859 |
0.861 |
0.874 |
0.868 |
0.859 |
0.892 |
0.875 |
0.892 |
0.859 |
0.877 |
0.86 |
0.885 |
Unit:gram
TABLE 1
 The sum of the 100 A&D Clips is 87.594g, and the average, 0.87594g. The standard deviation is 0.01632g while the maximum and minimum are 0.928g and 0.850g. GRAPH 1 shows the histogram or how they are distributed in weight.
The sum of the 100 A&D Clips is 87.594g, and the average, 0.87594g. The standard deviation is 0.01632g while the maximum and minimum are 0.928g and 0.850g. GRAPH 1 shows the histogram or how they are distributed in weight.
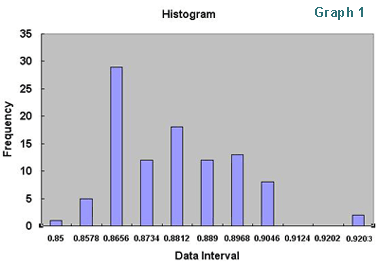
 I expected to see a better bell-shaped distribution pattern. It seems that 100 pieces was too small a quantity to always end up with a typical normal distribution pattern. Nevertheless let us work on this group of 100 pieces.
I expected to see a better bell-shaped distribution pattern. It seems that 100 pieces was too small a quantity to always end up with a typical normal distribution pattern. Nevertheless let us work on this group of 100 pieces.
 If a counting scale has the 0.87594gr that is the average of this group of 100 pieces registered as the piece weight, it will accurately display 100 pieces when all the clips are put on the pan. Therefore, the question for accurate and speedy counting will be how to get the registered piece weight to get closer to or equal to the 0.87594g weight without counting all the pieces. To show you this point, suppose the extreme case of you accidentally picking up the 10 pieces, which are the 10 pieces from the lightest as shown by the red bars in GRAPH 1, and place them on the pan to obtain the registered piece weight. The sum of those 10 pieces are 8.556g, thus the piece weight registered by the scale will be 0.8556g. Then you place the rest of the 90 clips on the pan. Since the sum of the 100 pieces in weight is 87.594g and the registered piece weight is 0.8556g, dividing 87.594g by 0.8556g gives a result of 102.377 or 102 pieces, which is incorrect, as the registered piece weight obtained has been biased to be lighter.
If a counting scale has the 0.87594gr that is the average of this group of 100 pieces registered as the piece weight, it will accurately display 100 pieces when all the clips are put on the pan. Therefore, the question for accurate and speedy counting will be how to get the registered piece weight to get closer to or equal to the 0.87594g weight without counting all the pieces. To show you this point, suppose the extreme case of you accidentally picking up the 10 pieces, which are the 10 pieces from the lightest as shown by the red bars in GRAPH 1, and place them on the pan to obtain the registered piece weight. The sum of those 10 pieces are 8.556g, thus the piece weight registered by the scale will be 0.8556g. Then you place the rest of the 90 clips on the pan. Since the sum of the 100 pieces in weight is 87.594g and the registered piece weight is 0.8556g, dividing 87.594g by 0.8556g gives a result of 102.377 or 102 pieces, which is incorrect, as the registered piece weight obtained has been biased to be lighter.
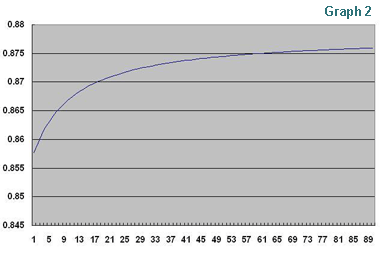
 If the registered piece weight is recalculated each time more pieces are added to the pan, the recalculated registered piece weight will change or get closer to the ultimate average piece weight for the group. In order to show this I added a piece to the first 10 pieces and recalculated the average weight for the whole and repeated this process 90 times. I used the average weight of the remaining clips that are not yet weighed, each time when I added a piece to the pan. The result of this is shown in GRAPH 2.
If the registered piece weight is recalculated each time more pieces are added to the pan, the recalculated registered piece weight will change or get closer to the ultimate average piece weight for the group. In order to show this I added a piece to the first 10 pieces and recalculated the average weight for the whole and repeated this process 90 times. I used the average weight of the remaining clips that are not yet weighed, each time when I added a piece to the pan. The result of this is shown in GRAPH 2.
 GRAPH 2 shows that the more pieces are added to calculate the average, the closer the average piece weight gets to the ultimate average weight of 0.87594g exponentially. This also indicates the fact that an error associated with a piece weight is inversely proportional to the square of the ratio of the number of samples applied. That is, if you use 2 times more samples, the error is reduced by 4 times.
GRAPH 2 shows that the more pieces are added to calculate the average, the closer the average piece weight gets to the ultimate average weight of 0.87594g exponentially. This also indicates the fact that an error associated with a piece weight is inversely proportional to the square of the ratio of the number of samples applied. That is, if you use 2 times more samples, the error is reduced by 4 times.
 When the total weight of this group of 100 pieces is divided by the average of the 10 pieces in the above case, the result was 102 pieces, which means the piece weight calculated by using the lightest 10 pieces was insufficient to extrapolate the total quantity of 100 pieces. However, we can extrapolate correctly a quantity larger than 10 pieces to a certain quantity by using this registered piece weight. Column 3 of TABLE 3 indicates this extrapolation can go correctly as far as to 28 pieces, but cannot extrapolate more than 29 pieces as the deviation of the registered piece weight from the average weight of the total clips on the pan becomes too great to count accurately.
When the total weight of this group of 100 pieces is divided by the average of the 10 pieces in the above case, the result was 102 pieces, which means the piece weight calculated by using the lightest 10 pieces was insufficient to extrapolate the total quantity of 100 pieces. However, we can extrapolate correctly a quantity larger than 10 pieces to a certain quantity by using this registered piece weight. Column 3 of TABLE 3 indicates this extrapolation can go correctly as far as to 28 pieces, but cannot extrapolate more than 29 pieces as the deviation of the registered piece weight from the average weight of the total clips on the pan becomes too great to count accurately.
 If the scale recalculates the registered piece weight by using the total weight of 28 pieces or any number of pieces between 11 and 28 pieces, the scale will have a piece weight closer to the ultimate piece weight for the whole group as demonstrated in GRAPH 2. The fourth column of TABLE 2 indicates the scale can accurately extrapolate the pieces of the clips on the pan as far as 81 pieces by using a piece weight recalculated with the 28 pieces. Then the registered piece weight is again recalculated using the 81 pieces on the pan, and it can go on to extrapolate correctly up to 100 pieces.
If the scale recalculates the registered piece weight by using the total weight of 28 pieces or any number of pieces between 11 and 28 pieces, the scale will have a piece weight closer to the ultimate piece weight for the whole group as demonstrated in GRAPH 2. The fourth column of TABLE 2 indicates the scale can accurately extrapolate the pieces of the clips on the pan as far as 81 pieces by using a piece weight recalculated with the 28 pieces. Then the registered piece weight is again recalculated using the 81 pieces on the pan, and it can go on to extrapolate correctly up to 100 pieces.
s |
s |
Average weight of 10 pieces |
Average weight of 28 pieces |
Average weight of 81 pieces |
s |
s |
0.8556 |
0.8701 |
0.8754 |
# of clips |
Total weight |
s |
s |
s |
11 |
9.4342 |
11 |
s |
s |
12 |
10.3124 |
12 |
s |
s |
13 |
11.1906 |
13 |
s |
s |
14 |
12.0688 |
14 |
s |
s |
15 |
12.947 |
15 |
s |
s |
16 |
13.8252 |
16 |
s |
s |
17 |
14.7034 |
17 |
s |
s |
18 |
15.5816 |
18 |
s |
s |
19 |
16.4598 |
19 |
s |
s |
20 |
17.338 |
20 |
s |
s |
21 |
18.2162 |
21 |
s |
s |
22 |
19.0944 |
22 |
s |
s |
23 |
19.9726 |
23 |
s |
s |
24 |
20.8508 |
24 |
s |
s |
25 |
21.729 |
25 |
s |
s |
26 |
22.6072 |
26 |
s |
s |
27 |
23.4854 |
27 |
s |
s |
28 |
24.3636 |
28 |
s |
s |
29 |
25.2418 |
30 |
29 |
s |
30 |
26.12 |
31 |
30 |
s |
31 |
26.9982 |
32 |
31 |
s |
32 |
27.8764 |
33 |
32 |
s |
33 |
28.7546 |
34 |
33 |
s |
34 |
29.6328 |
35 |
34 |
s |
35 |
30.511 |
36 |
35 |
s |
36 |
31.3892 |
37 |
36 |
s |
37 |
32.2674 |
38 |
37 |
s |
38 |
33.1456 |
39 |
38 |
s |
39 |
34.0238 |
40 |
39 |
s |
40 |
34.902 |
41 |
40 |
s |
41 |
35.7802 |
42 |
41 |
s |
42 |
36.6584 |
43 |
42 |
s |
43 |
37.5366 |
44 |
43 |
s |
44 |
38.4148 |
45 |
44 |
s |
45 |
39.293 |
46 |
45 |
s |
46 |
40.1712 |
47 |
46 |
s |
47 |
41.0494 |
48 |
47 |
s |
48 |
41.9276 |
49 |
48 |
s |
49 |
42.8058 |
50 |
49 |
s |
50 |
43.684 |
51 |
50 |
s |
51 |
44.5622 |
52 |
51 |
s |
52 |
45.4404 |
53 |
52 |
s |
53 |
46.3186 |
54 |
53 |
s |
54 |
47.1968 |
55 |
54 |
s |
55 |
48.075 |
56 |
55 |
s |
56 |
48.9532 |
57 |
56 |
s |
57 |
49.8314 |
58 |
57 |
s |
58 |
50.7096 |
59 |
58 |
s |
59 |
51.5878 |
60 |
59 |
s |
60 |
52.466 |
61 |
60 |
s |
61 |
53.3442 |
62 |
61 |
s |
62 |
54.2224 |
63 |
62 |
s |
63 |
55.1006 |
64 |
63 |
s |
64 |
55.9788 |
65 |
64 |
s |
65 |
56.857 |
66 |
65 |
s |
66 |
57.7352 |
67 |
66 |
s |
67 |
58.6134 |
69 |
67 |
s |
68 |
59.4916 |
70 |
68 |
s |
69 |
60.3698 |
71 |
69 |
s |
70 |
61.248 |
72 |
70 |
s |
71 |
62.1262 |
73 |
71 |
s |
72 |
63.0044 |
74 |
72 |
s |
73 |
63.8826 |
75 |
73 |
s |
74 |
64.7608 |
76 |
74 |
s |
75 |
65.639 |
77 |
75 |
s |
76 |
66.5172 |
78 |
76 |
s |
77 |
67.3954 |
79 |
77 |
s |
78 |
68.2736 |
80 |
78 |
s |
79 |
69.1518 |
81 |
79 |
s |
80 |
70.03 |
82 |
80 |
s |
81 |
70.9082 |
83 |
81 |
s |
82 |
71.7864 |
84 |
83 |
82 |
83 |
72.6646 |
85 |
84 |
83 |
84 |
73.5428 |
86 |
85 |
84 |
85 |
74.421 |
87 |
86 |
85 |
86 |
75.2992 |
88 |
87 |
86 |
87 |
76.1774 |
89 |
88 |
87 |
88 |
77.0556 |
90 |
89 |
88 |
89 |
77.9338 |
91 |
90 |
89 |
90 |
78.812 |
92 |
91 |
90 |
91 |
79.6902 |
93 |
92 |
91 |
92 |
80.5684 |
94 |
93 |
92 |
93 |
81.4466 |
95 |
94 |
93 |
94 |
82.3248 |
96 |
95 |
94 |
95 |
83.203 |
97 |
96 |
95 |
96 |
84.0812 |
98 |
97 |
96 |
97 |
84.9594 |
99 |
98 |
97 |
98 |
85.8376 |
100 |
99 |
98 |
99 |
86.7158 |
101 |
100 |
99 |
100 |
87.594 |
102 |
101 |
100 |
TABLE 2

I hope by now that you have come to see how ACAI works. It is the method to correctly extrapolate total pieces on the pan by using the previously registered piece weight and recalculating the registered piece weight by using the total pieces; so long as the total pieces on the pan are in the statistically safe zones for correct extrapolation so that the registered piece weight is recalculated and progresses to approach the ultimate piece weight of the group that extrapolate correctly the total number of clips on the pan.
 The most important issue with ACAI is how to impose the limits for the recalculation of the registered weight to be activated. I used the simplest example I could think of above to show how ACAI works. Thus, the actual ACAI has incorporated factors associated with the internal resolution and the empirical know-how so that the scale should always (we can only say statistically close to 100% of times) correctly recalculate the registered piece weight. In short, it is safe to say that you can double the total pieces on the pan each time and have the ACAI activated to recalculate the registered piece weight correctly.
The most important issue with ACAI is how to impose the limits for the recalculation of the registered weight to be activated. I used the simplest example I could think of above to show how ACAI works. Thus, the actual ACAI has incorporated factors associated with the internal resolution and the empirical know-how so that the scale should always (we can only say statistically close to 100% of times) correctly recalculate the registered piece weight. In short, it is safe to say that you can double the total pieces on the pan each time and have the ACAI activated to recalculate the registered piece weight correctly.
 I hope I have given you some basic understanding about how the ACAI works and the logic behind it, and would like to close this writing with one enlightening story.
I hope I have given you some basic understanding about how the ACAI works and the logic behind it, and would like to close this writing with one enlightening story.
 I used to get bewildered when I heard someone say that their counting machine must count 100% correctly all the time because his customers do not accept excess materials even by one piece, let alone a shortage. It did not sound practical, as accuracy must go with economics of making no errors. That is why we always have tolerance to work with. While we were discussing the problem of counting errors, Mr. Urata who worked as general manager at A&D Scientech Taiwan mentioned that an operator has to check all the circuit boards to see whether there are any boards with missing components when he ends up with a leftover component. The operator must have a 100% correct quantity of components so that he can avoid wasting hours checking all the circuit boards he worked on. Only then the 100% accuracy demand made sense. ACAI must have a great economical value!
I used to get bewildered when I heard someone say that their counting machine must count 100% correctly all the time because his customers do not accept excess materials even by one piece, let alone a shortage. It did not sound practical, as accuracy must go with economics of making no errors. That is why we always have tolerance to work with. While we were discussing the problem of counting errors, Mr. Urata who worked as general manager at A&D Scientech Taiwan mentioned that an operator has to check all the circuit boards to see whether there are any boards with missing components when he ends up with a leftover component. The operator must have a 100% correct quantity of components so that he can avoid wasting hours checking all the circuit boards he worked on. Only then the 100% accuracy demand made sense. ACAI must have a great economical value!
You may address any comments concerning this editorial by email to Mr. Eto
Index of Mr. Eto's other articles

